1. 引言
LLVM中诸多pass需要对控制流图进行分析、转化,因此引入了众多图论相关的算法与工具,典型的如dfs_iterator,post_order_iterator等各种遍历迭代器。在这些工具中,强连通分量迭代器(scc_iterator)功能强大,用途广泛(如判断callgraph中某个函数是否递归等),但其实现也相对复杂。本文将先介绍用于计算强连通分量的Tarjan算法,之后讲解scc_iterator的实现及其使用,帮助读者彻底掌握该工具。
2. 计算强连通分量
2.1 什么是强连通分量(SCC)?
有向图G中,如果子图U中的任意两点可达,那么就称U是一个强连通分量。如果不存在包含U的更大子图满足任意两点可达,那么就称U是极大的。一般而言,我们谈论的连通分量都是指极大连通分量。下图是一个有向图及其连通分量的例子。可以看到,如果将连通分量缩成一个点,那么原来的有向图就变成了一个DAG。
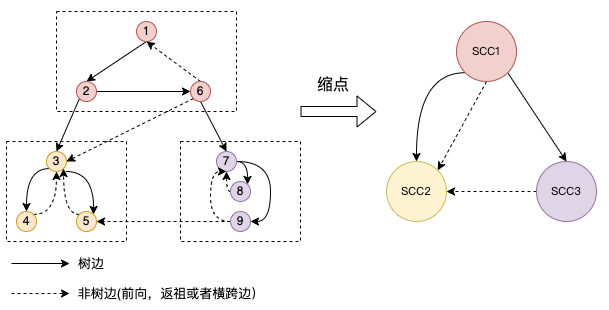
要证明缩点后的图是DAG也很简单,假设不是DAG,则有环,那么就能构成一个更大的连通分量,与缩点前每个连通分量是极大的矛盾。
2.2 强连通分量的根
如果我们给每个点v一个dfs的编号,记为\(dfn(v)\)。那么定义强连通分量中,\(dfn\)最小的点为这个分量的根。例如,在图1的例子中,SCC1的根是\(v_1\),SCC2与SCC3的根分别是\(v_3\)与\(v_7\)。不难发现,根是强连通分量中其余节点的祖先。
证明:
- 对于强连通分量中的任意一点\(v\),由定义知:存在根\(v_0\)到\(v\)的路径,且该路径上的所有节点都位于连通分量中。
- 不妨设该路径为\(v_0 \overset{p} \rightsquigarrow v\),因为\(v_0\)是根,所以它是该路径上的最小值,自然\(v_0 < v\)。
- 根据路径引理可知,存在该路径上的一点,是\(v_0\)与\(v\)的共同祖先。而内部节点以及\(v\)都大于\(v_0\),都不可能是公共祖先。
- 所以\(v_0\)是两者的公共祖先,也即\(v_0\)是\(v\)的祖先,证毕。
2.3 节点的lowlink值
对于任意点v,我们定义其\(lowelink\)值为:从点v出发,经过0或多条树边后,再经过至多一条返祖边或横跨边所能到达的连通分量内的点的最小编号。同时,我们定义符合该约束的路径为\(lowelink\ path\)。那么\(lowlink(v)\)就是所有\(lowlink\ path\)所能到达的点的最小值。
例如图1中,\(v_2\)的\(lowlink\ path\)有:\(v_2\),\(v_2 \rightarrow v_6\),\(v_2 \rightarrow v_6 \rightsquigarrow v_1\)。因此\(lowlink(v_2) = 1\)(注意\(v_2 \rightarrow v_6 \rightarrow v_7\)不是\(lowlnk\ path\),因为\(v_7\)不在\(v_2\)的连通分量内)。
因为每个点自身就是一个候选点,所以有\(lowlink(v) \leq dfn(v)\)。我们可以证明强连通分量中,根的\(lowlink\)等于自身的编号,其余节点的\(lowlink\)小于自身的编号。形式化描述如下:
\[\begin{align} lowlink(v) &= dfn(v) && 如果v是强连通分量的根\\ lowlink(v) &< dfn(v) && 否则 \end{align}\]证明:
- 因为根是强连通分量内的最小值,所以(1)显然成立。
- 对于非根节点v,根据强连通的定义,存在v到根节点\(v_0\)的路径\(v \overset{+p} \rightsquigarrow v_0\),且路径上所有的点都位于同一强连通分量中。
- 设v及其子孙所形成的子树是\(T_v\),\(a \rightsquigarrow b\)是路径p中第一条离开\(T_v\)的返祖边或者横跨边。
- 先证p中存在离开\(T_v\)的边。假设p无法离开\(T_v\),则p只能到达v的子孙。而又因为路径p中\(v_0\)是v的祖先,与假设矛盾。
- 再证该边是返祖边或者横跨边。因为树边或者前向边都是从祖先指向子孙节点,所以这两种边的终点位于起点所在的子树中。而根据上一步的证明,b不在a所处的子树\(T_v\)中,因此不可能是前向边或者树边,那么就只能是返祖边或者横跨边了。
- 如果\(a \rightsquigarrow b\)是返祖边,则b是a的祖先。考虑dfs树中从根到a的树路径:\(root \overset{*x} \rightarrow v_0 \overset{+y} \rightarrow v \overset{*z} \rightarrow a\)(\(v_0\)是强连通分量的根)。如果b位于z中,则v是b的祖先,b位于\(T_v\)中,矛盾。所以b只能位于x或者y中,即b是v的祖先。有\(dfn(b) < dfn(v)\)。
- 如果\(a \rightsquigarrow b\)是横跨边,则a,b位于不同的子树且\(a > b\)。设m是a,b的最近公共祖先,仍然考虑dfs树中从根到a的树路径:\(root \overset{*x} \rightarrow v_0 \overset{+y} \rightarrow v \overset{*z} \rightarrow a\),因为m是a的祖先,所以m位于x,y或者z中。如果m位于z中,则v是m的祖先,进而有v是b的祖先,可以推出b位于\(T_v\)中,矛盾。所以m只能位于x或者y中,也即m是v的祖先。因为dfs树中,某个点的右子树上的任意一点都大于左子树,而\(a > b\),所以a相对于b而言位于m的右子树,b位于m的左子树。再加上v是a的祖先,且是m的子孙,因此v与a位于m的同一个右子树中,有\(dfn(b) < dfn(v)\)。
- 因此对于\(a\rightsquigarrow b\),有\(dfn(b) < dfn(v)\)。
- 因为a位于\(T_v\)中,所以存在树路径\(v \overset{*} \rightarrow a\),那么加上边\(a\rightsquigarrow b\),我们得到了一条v的\(lowlink\ path\):\(v \overset{*} \rightarrow a \rightsquigarrow b\)。所以有\(lowlink(v) \leq dfn(b) < dfn(v)\)。(2)式成立,证毕。
2.4 lowlink的计算
根据定义,我们可以马上设计出一种算法:对于节点v,我们初始化\(lowlink(v) = dfn(v)\),然后遍历它的所有\(lowlink\ path\),不断更新\(lowlink(v)\)为更小值。那么遍历完之后就能得到\(lowlink(v)\)了。
算法的正确性是显然的,它几乎就是对定义的直接翻译,我们需要处理的就是如何遍历点v的\(lowlink\ path\),并更新\(lowlink(v)\)。
考虑点v的所有出边,设其为\(v \rightsquigarrow w\)。那么有如下几种情况:
- \(v \rightsquigarrow w\)是树边,且w与v在同一个强连通分量中。则任意经过该边的\(lowlink\ path\)就是该边拼接w的一条\(lowlink\ path\)。使用\(min(lowlink(v), lowlink(w))\)更新\(lowlink(v)\);
- \(v \rightsquigarrow w\)是树边,且w与v不在同一个强连通分量中。则不存在经过该边的\(lowlink\ path\),且w是另一个强连通分量的根,满足\(lowlink(w) = dfn(w) > dfn(v) \ge lowlink(v)\)。因此可以与情形1合并(跳过连通分量的判断)而不影响最终的结果;
- \(v \rightsquigarrow w\)不是树边,且w与v在同一个强连通分量中。那么经过该边的唯一\(lowlink\ path\)就是该边本身,使用\(min(lowlink(v), dfn(w))\)更新\(lowlink(v)\);
- \(v \rightsquigarrow w\)不是树边,且w与v不在同一个强连通分量中。则不存在经过该边的\(lowlink\ path\)。跳过,无需处理。
用伪代码描述以上单点lowlink的计算过程如下:
calculate_single_lowlink(v, G) // v is the point to be calculated, G is the graph
lowlink[v] = dfn[v];
for (v, w) in G
if (v, w) is a tree edge // case 1,2
lowlink[v] = min(lowlink[v], lowlink[w]);
else if w is in the same SCC with v // case 3
lowlink[v] = min(lowlink[v], dfn[w]);
该算法的其余部分比较简单,但是要判断v,w是否位于同一个强连通分量则较为复杂。Tarjan提出了一种算法,通过维护一个栈来判断一条边是否跨强连通分量,如果遍历到非树边,目标节点位于栈中,则属于同一个scc,否则跨scc。相关算法见下一节。
2.2 Tarjan算法
该算法只需一次dfs就能计算图的所有连通分量以及每个节点的\(lowlink\)。其伪代码如下:
TarjanDFS(v)
dfn[v] = lowlink[v] = ++timestamp; // initialize dfn and lowlink of node v
visit[v] = true;
stack.push(v);
for (v, w) in G
if visit[w] is false // tree edge
TarjanDFS(w);
lowlink[v] = min(lowlink[v], lowlink[w]); // lowlink case1, 2
else if w is in stack // case 3
lowlink[v] = min(lowlink[v], dfn[w]);
// now lowlink[v] is calculated
if lowlink[v] == dfn[v] // root of scc
while dfn[stack.top()] >= dfn[v]
stack.pop(); // all poped node is in the same scc rooted at v
算法的关键是引入了一个栈。当dfs到一个新点时将其入栈,回溯时计算每个点的\(lowlink\)值,如果该点的\(lowlink\)等于\(dfn\)(即该点是一个SCC的根),将该点以及栈顶之间的点弹出。弹出的点构成一个强连通分量。我们现在来证明该算法的正确性。
证明:
- 先证明无子连通分量的scc是对的。
- 记该连通分量为C,并设其第一个回溯点是v。由于v无树边(第一个回溯点是叶子节点),并且不存在跨scc的非树边,因此v只有同scc的非树边(2.4节的情形3)。该情形下,非树边的目标节点已经访问过,会入栈,且v之前未回溯过,无出栈操作,所以可以根据目标点是否在栈中来判断情形3,进而正确计算\(lowlink(v)\)。
- 假设前n个回溯点的\(lowlink\)能被正确计算。考虑第n+1个回溯点。如果该点存在树边,则树边的目标结点必然位于前n个回溯点中,而根据假设它们都被正确计算,因此2.4节中的情形1,2能被正确处理;如果该点存在位于相同scc的非树边, 由于前n个点(非根)被正确计算,不会有出栈操作,所以检测边的目标点在栈中可以判断情形3;而由于C不存在情形4,所以算法能正确计算第n+1个回溯点,即前n+1个回溯点都被正确计算。
- 由数学归纳法可知,该算法对C中所有回溯点都能正确计算。并且在回溯到C的根节点时,C中的所有节点被正确弹出!
- 假设scc的所有子scc都能被正确计算,则可推出该scc也能被正确计算。
- 证明与之前类似。记该scc为C,设v是C中的第一个回溯点。如果v存在树边,那么必然是连接某个子scc,由于子scc被正确计算,因此2.4节中的情形1,2被正确计算;如果v存在位于相同scc的非树边,由于出栈的只可能是子scc,所以可以检测目标节点在栈中来匹配情形3;如果v存在跨不同scc的非树边,那么只可能是到子scc的边,而任何子scc都已先于C被回溯以及出栈,所以可以检测目标点不在栈中来判断情形4。结合这几种情形,v能被正确计算。
- 假设C中前n个回溯点被正确计算。考虑第n+1个回溯点,如果该点存在树边,则其子节点要么位于前n个回溯点中,要么位于某个子scc,而这两者都先于该点被正确回溯处理,因此2.4节中的情形1,2被正确计算;如果该点存在位于相同scc的非树边,由于只有子scc可能已经出栈,因此可检测目标点在栈中判断情形3;如果该点存在跨scc的非树边,则只能是到子scc的边,由于子scc先被回溯且被正确弹出,检测目标点不在栈中可以识别情形4。结合这几点,可以推出第n+1个回溯点被正确计算,即位于C中的前n+1个回溯点被正确计算。
- 由数学归纳法可知,C中的节点被正确计算,且被正常出栈。
- 由数学归纳法可知,所有scc中的节点都能被正确计算,因此算法正确。
3. scc_iterator的实现
scc_iterator能以scc DAG的逆拓扑序方式返回scc。并且返回的scc中按照编号由大到小降序排列(根在最后)。该迭代器采用了Tarjan算法进行实现,但是为了保存迭代状态,采用了栈形式的dfs。同时对非树边的处理也略有不同。
3.1 用栈实现dfs
由于dfs无法记录迭代过程的状态,需要用到栈形式的dfs。在这种实现中,入栈出栈操作与递归调用栈类似,每dfs到一个新点就入栈,回溯完一个点就出栈。为了记住每个节点还有那些子节点没有处理,每个栈元素保存了一个子节点迭代器,指向还未遍历到的子节点,只有当子节点迭代器无效时,该点才能回溯。下面就是scc_iterator中的的栈元素数据类型:
struct StackElement {
NodeRef Node; // 当前节点
ChildItTy Child; // 下一个要遍历的子节点
unsigned MinVisited; // lowlink
};
用栈实现dfs的思路如下:
StackDFS(v)
stack.push(StackElement{v, v.first_child, ...})
while stack is not empty
while stack.top().Child is valid // v 还有未遍历的子节点
CurrChild = stack.top().Child;
++stack.top().Child; // 更新child为下一个子节点
if CurrChild is not visited
stack.push(StackElement{CurrChild, CurrChild.first_child, ...}); // 子节点入栈,表示dfs到下一个节点
// 回溯
stack.pop(); // 弹出当前节点
3.2 lowlink的更新
scc_iterator并没有设置一个专门的数据结构判断某个已访问点是否在栈中,而是将已出栈的scc节点的\(dfn\)值设为无穷大(~0U)。这样可以用\(lowlink(v) = min(lowlink(v), dfn(w))\)直接处理非树边从而跳过是否在栈中的判断。
StackTarjan(v)
stack.push(StackElement{v, v.first_child, ++visitNum}); // dfs栈
while stack is not empty
while stack.top().Child is valid
CurrChild = stack.top().Child;
++stack.top().Child;
if CurrChild is not visited
++visitNum;
SCCNodeStack.push(CurrChild); // Tarjan算法维护的栈
nodesVisitNum[CurrChild] = visitNum;
stack.push(StackElement{CurrChild, CurrChild.first_child, visitNum});
else
stack.top().MinVisited = min(stack.top().MinVisited, nodesVisitNum[CurrChild]); // CurrChild如果不在栈中,其值为无穷,不影响结果
// 回溯
lowlink = stack.top().MinVisited;
node = stack.top().Node;
stack.pop();
// 更新父节点
if stack is not empty
stack.top().MinVisited = min(stack.top().MinVisited, lowlink);
// 判断是否是根
if lowlink is equial to nodesVisitNum[node]
do
CurrentSCC.push_back(SCCNodeStack.top());
SCCNodeStack.pop();
nodeVistiNum[CurrentSCC.back()] = ~0U; // 出栈的点设为无穷
while CurrentSCC.back() is not node